Teoreticke´ rešenı strech. Katedra didaktiky matematiky. Aplikace matematiky pro ucitele, 13. Vyřešte střechu nad daným půdorysem, za předpokladu, že okapy leží v jedné vodorovné rovině a střešní roviny mají stejný spád.
Pozor na nepovolené vodorovné úžlabí neboli žlab! Při řešení střech bude třeba v pravoúhlém promítání vyřešit úlohy o.

Při teoretickém řešení budeme předpokládat (jestliže neurčíme jinak), že: ○ Všechny okapy jedné budovy leží v jedné horizontální rovině. Roviny střechy svírají s touto horizontální rovinou stejné úhly, jsou tedy téhož spádu, v našem případě platí tgα = = tg45°. Každým okapem prochází jedna rovina . Různé možnosti řešení střechy Často se nám naskytne několik možností správného řešení střechy. Rozhodující je potom stanovisko praktického zhotovení vlastní střechy nebo stanovisko estetického vzhledu střechy. Průsečnice rovin – užití.
Nejčastěji se vyskytující střechou je střecha sedlová. SPŠ stavební a Obchodní. Vyřešte valbovou střechu nad tímto půdorysem tvaru „EL“.

Půdorys doplňte o nárys, sklon střechy volte °. Deskriptivní geometrie 2. Metodou číslování vyřešte střechu nad daným půdorysem. Střešní roviny mají stejný spád roven 1. Sestrojte nárys a kosoúhlý průmět střechy. Geometrické řešení půdorysů střech. Pojmy týkající se teoretického řešení střech.
Základní principy využívané při konstrukci půdorysů sklonitých střech stejného spádu. Konstrukce půdorysů sklonitých střech. Základní sklonité střechy – zastřešení obdélníkového půdorysu. Program je určen k teoretickému řešení střech – k zadanému půdorysu budovy spočítá a vykreslí odpovídající zastřešení. Použité technologie: Turbo Pascal 7. Seznam elaborátů k zápočtu.
Kosoúhlé promítání je který je poměrem délky prům zkrácení – prodloužení. Střecha Je stavební konstrukce, která shora ukončuje stavbu a chrání ji před povětrnostními vlivy Dělí se na: a) nosnou konstrukci – krov, statická funkce b) střešní plášť – izolace, ochranná funkce Rozdělení střech : 1. Podle tvaru – rovinné – rotační – zborcené 2. Podle sklonu – ploché 0°-5°(10°) – šikmé 5°-10°-° – strmé . Cílem sady je seznámení žáků s principy kosoúhlého .
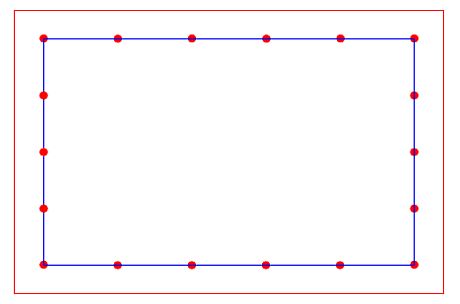
Dobrý den, vím že je to matematické forum, ale pevně věřím, že se zde najdou i experti na deskriptívu. Kdyby byl někdo tak ochotný a vyřešil mi tu střechu a třeba oskenoval, byl bych moc vděčný.